Question

If AB < AC < CB in triangle ABC then which of the following is true?

Angle A < Angle B < Angle C
Angle C < Angle A < Angle B
Angle C < Angle B < Angle A
Angle A < Angle C < Angle B,

Answer 1

The answer would be the third option where angle C is the smallest while angle A is the largest. For example, in a 30-60-90 triangle the hypotenuse (2x) uses angles 30 and 60 which are smaller than 90. Then the smaller leg (x) uses angles 60 and 90 while the larger leg (x
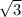
`√(3)`) uses angles 30 and 90. I hope this helped!

Answer 2

Angle C < Angle B < Angle A

For this problem, the sides opposite each angle is proportional to the sine of the angle. Larger side = larger angle. So we've been given AB < AC < CB.
Side AB is opposite angle C

Side AC is opposite angle B
Side CB is opposite angle A
So
C < B < A

Now looking at the options, the third options matches, which is
Angle C < Angle B < Angle A

The other 3 options don't match and therefore are wrong.