Question

Which ordered pair could be removed so that the resulting graph represents a function

Answer 1

One of this ordered pairs:
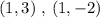`\left ( 1,3 \right )\,,\,\left (1 ,-2 \right )` should be removed

Explanation:

A relation f is said to be a function if for each and every element of it's domain there exists a unique image in it's codomain.

As per the graph, ordered pairs are
`\left ( 1,3 \right )\,,\,\left ( 2,1 \right )\,,\,\left ( -2,2 \right )\,,\,\left (1 ,-2 \right )\,,\,\left ( 5,-4 \right )\,,\,\left ( -4,-4 \right )\,,\,\left ( -5,-3 \right )`

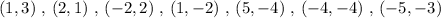
Here, all the ordered pairs have unique image except
`\left ( 1,3 \right )\,,\,\left (1 ,-2 \right )`

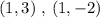
Here , element 1 of domain has two images 3 and - 2 .

We know that as per definition for each and every element of the domain there should be a unique image in the codomain.

So, one of this ordered pairs:
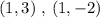`\left ( 1,3 \right )\,,\,\left (1 ,-2 \right )` should be removed in order to make it a function.

Answer 2

The relation is double-valued for x=1. Removing either of those values will make the relation a function.
.. (1, -2)
or
.. (1, 3)