Answer:
A.
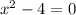
D.
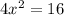
Explanation:
To check which of the given equations have solution
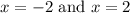 , we will solve our given equations one by one.
, we will solve our given equations one by one.
A.
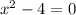
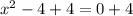
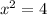
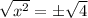

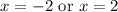
Therefore, option A is the correct choice.
B.
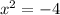
To solve our given equation, we need to take square root of both sides of equation. Since square root is not defined for negative numbers, therefore, option B is not a correct choice.
C.
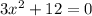
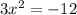
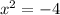
To solve our given equation, we need to take square root of both sides of equation. Since square root is not defined for negative numbers, therefore, option C is not a correct choice.
D.
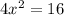
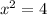
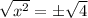

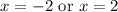
Therefore, option D is the correct choice.
E.
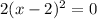
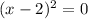
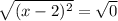
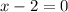
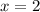
Therefore, option E is not a correct choice.