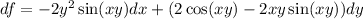Question

Find the differential of the function. v = 2y cos(xy)

Answer 1

Given a function f(x,y), the differential of f is given by

`df = f_x dx + f_y dy`
where
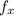
`f_x` is the derivative of f(x,y) with respect to x, while
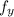
`f_y` is the derivative of f(x,y) with respect to y.

The function of our problem is
`f(x,y)=2y \cos(xy)`
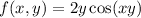
The derivative in x is

`f_x = 2y(-y \sin (xy))=-2y^2 \sin (xy)`
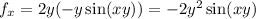
The derivative in y is

`f_y = 2 \cos (xy) + 2y (-x \sin (xy))=2 \cos (xy) - 2xy \sin (xy)`

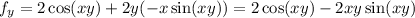
So, the differential of f(x,y) is

`df= -2y^2 \sin (xy) dx + (2 \cos (xy) - 2xy \sin (xy))dy`