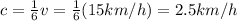Question

A motorboat, whose speed in still water is 15 km/hour, traveled with the current of a river for 35 km, and against the current for 25 km. the boat took the same time traveling with the current as it did traveling against the current. what is the speed of the current in the river?

Answer 1

Let's call v=15 km/h the speed of the boat in still water, and c the speed of the current.
When the boat travels with the current, its total speed is (v+c), and it travels for a distance of 35 km in a time t. When the boat travels against the current, its total speed is (v-c), and it travels for a distance of 25 km in the same time t. We can write the basic relationship of the uniform linear motion
`S=vt` for both situations:

`35 km = (v+c)t`

`25 km=(v-c)t`
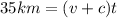
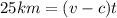
If we divide the first equation by the second one, we find

`(35)/(25)= (v+c)/(v-c)`
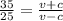
and by rearranging this, we can find the value of c, the speed of the current:

`c= (1)/(6)v= (1)/(6)(15 km/h)=2.5 km/h`