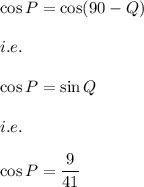Question

In right triangle PQR, P and Q are complementary angles. The value of sin Q is 9/

41
. What is the value of cos P?

Will be given brainley

Answer 1

Option: A is the correct answer.

The value of cos P is:

A)
`(9)/(41)`

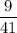
Explanation:

We know that if two angles A and B are complementary then,

`A+B=90`

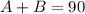
i.e.

`B=90-A`

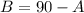
Here we have angle P and angle Q are complementary i.e.

`P=90-Q`

Also, we are given,

`\sin Q=(9)/(41)`

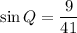
We are asked to find:

`\cos P`

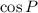
It could also be written as:

`\cos P=\cos (90-Q)\\\\i.e.\\\\\cos P=\sin Q\\\\i.e.\\\\\cos P=(9)/(41)`

Answer 2

All that given means is they add up to 90o. They must since the triangle is a right triangle.
That's my LOL for the night. It's very late where I am. Probably where you are too.
Draw the diagram. This is a very important question. I don't want to just tell you because in many disguises, this problem shows up more than once. So draw the diagram.

Put the Sin of Q in. Sin(Q) is PR/QP Label PR as 9 and QP is 41. Make sure you agree with me before reading the rest.

Do you agree? Good you can go on.
Now go down to <RPQ. A cosine is the adjacent side over the hypotenuse. What I was giggling about when I saw it was that the Cos of P is the Same as the Sin(Q). This fact is going to turn up many times in many different forms. Of all the questions you've asked tonight, this is the one you must pay the closes attention to.

9/41 = Cos P <<<<==== Answer.