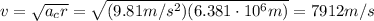The centripetal force for an object moving in circular motion is:
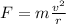
where m is the mass, v the speed of the object and r the radius of the orbit. For Newton's second law, this is equal to
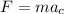
where
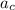
is the centripetal acceleration. So we can find the centripetal acceleration by equalizing the two equations:

Since we know the value of the centripetal acceleration of the rocket,
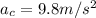
, and the radius of the orbit,
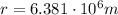
, we can solve the previous formula for v, the speed of the rocket: