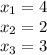One root of f(x)=x^3-9x^2+26x-24 is x = 2. What are all the roots of the function?

Question

asked May 1, 2019 50.9k views

2 Answers

ASpencer · Answer 1 · 2019-05-08T02:46:14+0000

Answer:

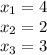
$x_(1)=4\\x_(2)=2\\ x_(3)=3$

Explanation:

The given expression is

f(x)=x^(3)-9x^(2) +26x-24

First, we need the divisors of the independent term, which is 24.

24 divisors: 1, 2, 3, 4, 6, 8, 12, 24.

Now, we replace each divisor in the function, and those which gives zero as result, those are gonna be the roots of the equation.

For
x=1

f(1)=(1)^(3)-9(1)^(2) +26(1)-24=1-9+26-24=-6

This means
x=1 is not a solution.

For
x=2

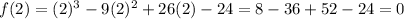
f(2)=(2)^(3)-9(2)^(2) +26(2)-24=8-36+52-24=0

So,
x=2 is the first solution.

For
x=3

f(3)=(3)^(3)-9(3)^(2) +26(3)-24=27-81+78-24=0

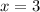
It's solution.

For
x=4

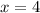
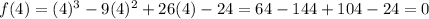
f(4)=(4)^(3)-9(4)^(2) +26(4)-24=64-144+104-24=0

Therefore, all roots are

$x_(1)=4\\x_(2)=2\\ x_(3)=3$