Question

One of the parking lot lights at a hospital has a motion detector on it, and the equation (x+10)2+(y−8)2=16 describes the boundary within which motion can be sensed.

What is the greatest distance, in feet, a person could be from the parking lot light and be detected?

Answer 1

Yes the correct answer is 4ft
because the radius of that circle is 4
(x+10)^2+(y−8)^2=4^2
Thanks Rodiak

Answer 2

We are given an equation:

`(x+10)^(2) + (y-8)^(2) = 16`

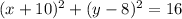
This is an equation of a circle. General form of a circle equation is:

`(x-a)^(2) + (y-b)^(2) = r^(2)`
Where:
a = x coordinate of a center
b = y coordinate of a center
r = radius of a circle

Motion detector can detect person anywhere within a boundary. The greatest distance at which detector can detect is at the edge of a circle. That distance, between detector and edge of circle, is equal to radius.

From the equation we have:

`r^(2) =16 \\ r=4`
The greatest distance at which person can be detected is 4ft.