Question

X^2+19=10 solve algebraically
4x^2+3=43 solve algebraically

Answer 1

`a)\ x_1=-3i,\ x_2 =3i`

`b)\ x_1=-√(10),\ x_2=√(10)`

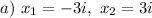
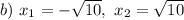
Explanation:

Given equations:

`a)\ x^2+19=10\\\\b)\ 4x^2+3=43`

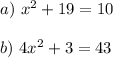
A. x² + 19 = 10

Step 1: Subtract 19 from both sides.

`\\\implies x^2+19-19=10-19\\\\\implies x^2=-9`

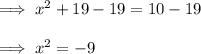
Imaginary number rule: For any positive real number "k",
`√(-k) = i√(k)`

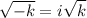
Note: Two imaginary (complex) solutions indicate that the graph will not intersect the x-axis. As a result, it has no real roots.

Step 2: Take the square root of both sides (positive and negative roots).

`\\\implies √(x^2)=√(-9)\\\\\implies x=\pm\ i√(9)\\\\\implies x=\pm\ 3i`

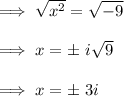
Step 3: Separate the solutions.

`\implies x_1=-3i,\ x_2 =3i`

----------------------------------------------------------------------------------------------------------------

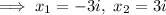
B. 4x² + 3 = 43

Step 1: Subtract 43 from both sides.

`\\\implies 4x^2++3-3=43-3\\\\\implies 4x^2=40`

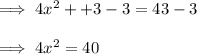
Step 2: Divide both sides by 4.

`\\\implies 4x^2=40\\\\\implies \frac{4x^2}4=(40)/(4)\\\\\implies x^2=10`

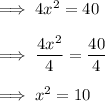
Step 3: Take the square root of both sides (positive and negative roots).

`\\\implies √(x^2)=√(10)\\\\\implies x=\pm\ √(10)`

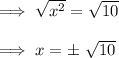
Step 4: Separate the solutions.

`\implies x_1=-√(10),\ x_2=√(10)`