Question

What is the half-life (in seconds) of a zero-order reaction which has an initial reactant concentration of 0.884 M with a k value of 5.42 × 10–2 M/s?

Answer 1

The half-life (in seconds) of a zero-order reaction is 8.15 seconds.

Step-by-step explanation:

Initial concentration of the of the reactant =
`[A_o]=0.884 M`

The value of rate constant =
`k=5.42* 10^(-2) M/s`

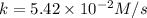
The half life for zero order reaction is given as:

`t-{(1)/(2)}=([A_o])/(2k)=(0.884 M)/(2* 5.42* 10^(-2) M/s)=8.15 s`

The half-life (in seconds) of a zero-order reaction is 8.15 seconds.

Answer 2

Answer: 8.15s


Step-by-step explanation:


1) A first order reaction is that whose rate is proportional to the concenration of the reactant:


r = k [N]


r = - d[N]/dt =


=> -d[N]/dt = k [N]


2) When you integrate you get:


N - No = - kt


3) Half life => N = No / 2, t = t'


=> No - No/ 2 = kt' => No /2 = kt' => t' = (No/2) / k


3) Plug in the data given: No = 0.884M, and k = 5.42x10⁻²M/s


t' = (0.884M/2) / (5.42x10⁻²M/s) = 8.15s