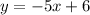Question

Write the slope-intercept form of an equation of the line that passes through (2,-4) and (0,6)

Answer 1

Hey there!

In order to write the slope-intercept form, we have to have slope, and the y intercepts, just as it says in the name. In order to find slope with two points, we use our formula:

y2-y1/x2-x1 =
6-(-4)/0-2 = 6+4/-2 =
10/-2 = -5

Now that we know our slope is negative five, we can use one of those poins to model our slope intercept form, y= mx+b, using our slope, to solve for b, our y intercepts. We'll use (0,6).

We have:

6 = -2(0) + b
6 = 0 + b
6 = b

Now, since we have the slope and y intercept, we can write the equation:

y = -2x + 6

Hope this helps!

Answer 2

we know that

the equation of the line in the slope-intercept form is equal to

`y=mx+b`

where

m is the slope of the line

b is the y-intercept of the line

Let

`A(2,-4)\\B(0,6)`

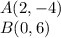
Step
`1`

Find the slope of the line AB

the slope between two pints is equal to

`m=((y2-y1))/((x2-x1))`

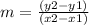
substitute the values

`mAB=((6+4))/((0-2))`

`mAB=((10))/((-2))`

`mAB=-5`

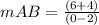
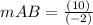
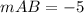
with the slope m and the point B find the value of b

`B(0,6)`

`6=-5*0+b`

`b=6`

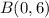
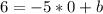
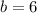
Find the equation of the line

`y=mx+b`

`y=-5x+6`

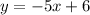
therefore

the answer is

`y=-5x+6`