Writing
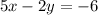 in slope-intercept form:
in slope-intercept form:
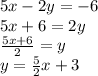
The slope of the line is the number before "x", which is
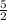 .
.
The slope of the perpendicular to this line is the negative reciprocal of this.
So the slope of perpendicular is
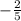 .
.
To find the equation of the perpendicular line, we need a point. It is given as
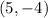 where
where
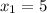 and
and
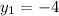 .
.
Now we use the point-slope form of a line to figure out the equation:
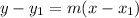
Plugging in the values of
 and
and
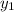 and
and
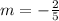 , gives us:
, gives us:
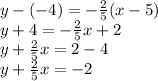
Multiplying everything by 5 [to get rid of the denominator] and re-arranging gives us:
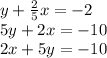 .
.
THIS IS THE SECOND OPTION.
ANSWER:
