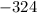Question

For the following geometric sequence find the recursive formula and the 5th term in the sequence. In your final answer, include all of your work.

{-4, 12, -36, ...}

Answer 1

First you need to identify the common ratio:

r =
`t_(n+1) / t_(n)`

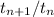
where r is the common ratio

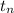
`t_(n)` is any term in the sequence

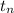
`t_(n)` is the term preceding
`t_(n)`

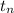
In your case the common ratio will be
12/-4 = -3
The recursive formula of a geometric sequence is:

An =
`A_(n-1)` x r
Where : An is the nth term

`A_(n-1)` is the erm preceding the nth term
r = common ratio

For this case it is:
An =
`A_(n-1)` x -3

Now let us use this formula to find the 5th term:


`A_(5)` =
`A_(5-1)` x -3

`A_(5)` =
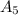
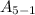
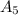
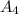
`A_(4)` x -3

Since you do not know the 4th term, you can use that by using our reclusive formula:


`A_(4)` =
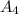
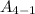
`A_(4-1)` x -3

`A_(4)` =
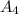
`A_(3)` x -3

`A_(4)` =
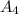
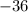
`-36` x -3

`A_(4)` =
`108`

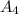
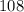
Now that you know your fourth term, you can use the same formula:


`A_(5)` =
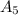
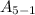
`A_(5-1)` x -3

`A_(5)` =
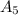
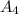
`A_(4)` x -3

`A_(5)` =
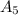
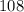
`108` x -3

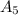
`A_(5)` =
`-324`

Answer 2

we have a geometric sequence----------- > {-4, 12, -36, ...}

the formula is a(r)^(n-1)

a------------- >a is the first term------------ > -4
r--------------- > is the common ratio------- > 12/(-4)=(-36/12)=-3
n--------------- > is the number of terms

The fifth term is -4[(-3)^(5-1)]=-4[(81]=-324

the answer is -324