Answer:
1.
 and
and
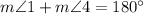 ; given
; given
2.
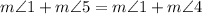 ; substitution
; substitution
3.
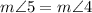 ; subtraction property of equality
; subtraction property of equality
4. Ray YZ is parallel to ray UV; if alternate interior angles equal , then lines are parallel.
Explanation:
Given

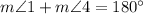
To prove that YZ is parallel to UV.
Proof:
1.Statement:
 and
and
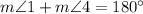
Reason; Given
2. Statement:
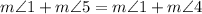
Reason: By using substitution property
3.Statement:
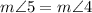
Reason: Subtraction property of equality.
4.Statement: Ray YZ is parallel to Ray UV
Reason: If alternate interior angles equal, then lines are parallel.