The surface charge density of a circular disk is given by the following relationship:
σ =
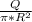
-- (A)
Where,
σ = Surface charge density.
Q = Charge on the surface
R = Radius of the circular disk.
Now according to the above equation, we can infer:
1) Surface charge density σ is directly proportional to the Charge Q on the surface of the disk.
2) Surface charge density σ is inversely proportional to the square of Radius R of the circular disk.
As the charge is 24nC on the circular disk, and there is no evidence of charge being changed in the question, I would assume that the charge is constant.
Let's apply the condition:
If R = 2R(if the radius of the disk is made doubled)
Plug in the value in (A):
A => σ(new) =
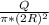
Therefore,
σ(new) =

Hence,
σ(new) = (1/4)σ
Conclusion:If the Radius of the disk is doubled, the new surface charge density would become one-fourth of the old surface charge density. Hence,
σ(new) =
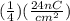 Ans: σ(new) = 6nC/
Ans: σ(new) = 6nC/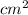
-i