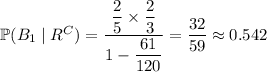Question

Box i contains 4 red and 8 blue marbles while box ii contains 5 red and 3 blue marbles. an unfair coin is tossed –whose probability of turning up heads is 40%. if the coin comes up heads box i is chosen and a random marble is chosen, otherwise if it is tails the marble is chosen from box ii.(a)find the probability a red marble is chosen.(b)if a red marble is chosen, what is the probability it came from box i? (c)if a blue marble is chosen, what is the probability it came from box i?

Answer 1

Denote by
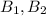
`B_1,B_2` the event that a marble is drawn from box 1 or 2, respectively, and by
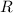
`R` the event that a red marble is drawn. If a blue marble is drawn, we'll denote that by the complement of
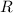
`R`, or
`R^C`.

a. If a red marble is drawn, either it's drawn from box 1 or box 2. The events
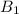
`B_1` and
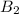
`B_2` are mutually exclusive, so we have


`\mathbb P(R)=\mathbb P((R\cap B_1)\cup(R\cap B_2))=\mathbb P(R\cap B_1)+\mathbb P(R\cap B_2)`

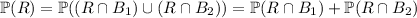
Now invoke the definition of conditional probability:


`\mathbb P(R)=\mathbb P(B_1)\mathbb P(R\mid B_1)+\mathbb P(B_2)\mathbb P(R\mid B_2)`

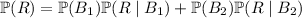
We're explicitly given the probability of drawing from either box. We also know the probabilities of drawing a red marble from box 1 or 2 are, respectively,


`\mathbb P(R\mid B_1)=\frac{\dbinom41\dbinom80}{\dbinom{12}1}=\frac4{12}=\frac13`

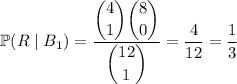
and


`\mathbb P(R\mid B_2)=(\dbinom51\dbinom30)/(\dbinom81)=\frac58`

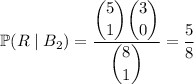
So


`\mathbb P(R)=\frac25*\frac13+\frac35*\frac58=(61)/(120)\approx0.508`

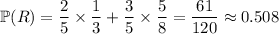
b. Given that we draw a red marble, we're looking for the probability that it was drawn from box 1, i.e.
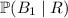
`\mathbb P(B_1\mid R)`. We use Bayes' theorem:


`\mathbb P(B_1\mid R)=(\mathbb P(B_1\cap R))/(\mathbb P(R))=(\mathbb P(B_1)\mathbb P(R\mid B_1))/(\mathbb P(R))`

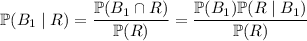
which is really just a matter of using the definition of conditional probability to rewrite the numerator on the the right side, as


`\mathbb P(R\cap B_1)=\mathbb P(R)\mathbb P(B_1\mid R)=\mathbb P(B_1)\mathbb P(R\mid B_1)`

We know
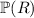
`\mathbb P(R)` from part (a), so we compute


`\mathbb P(B_1\mid R)=(\frac25*\frac13)/((61)/(120))=(16)/(61)\approx0.262`

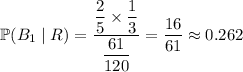
c. Now we look for
`\mathbb P(B_1\mid R^C)`, which can be computed similarly.


`\mathbb P(B_1\mid R^C)=(\mathbb P(B_1\cap R^C))/(\mathbb P(R^C))=(\mathbb P(B_1)\mathbb P(R^C\mid B_1))/(1-\mathbb P(R))`

`\mathbb P(B_1\mid R^C)=(\frac25*\frac23)/(1-(61)/(120))=(32)/(59)\approx0.542`