Answer:
Net horizontal force,
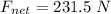
Step-by-step explanation:
It is given that,
Mass of the box, m = 50 kg
The coefficient of kinetic friction between the box and the ground is 0.35,

Acceleration of the box,
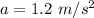
We know that the frictional force acts in opposite direction to the direction of motion. The net force acting on it is given by :
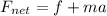
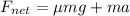
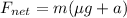

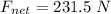
So, the net force acting on the box is 231.5 N. hence, this is the required solution.