Question

Please help, I honestly have no clue what I’m doing.

Given the table below, determine the following

Y = -4x+15

(Picture below)

Answer 1

y=-1

y=43

x=14

Explanation:

So, you have the equation:
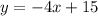`y=-4x+15`, and if we know one value we can easily solve for the other using some algebraic manipulation.

Find y when x=4.

For this we know one value, "x", and the other "y" value is unknown. This is actually not to hard if you notice that the equation we're given expresses the value of "y" in terms of "x".

So let's plug in the x-value:
`y=-4(4)+15\implies y=-16+15=-1`

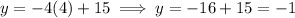
So we get: y=-1, which turns out to be the solution!

Find y when x=-7

This is a similar process, so let's just get straight into it and plug x as -7

`y=-4(-7)+15\\y=28+15\\y=43`

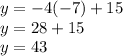
This is our solution, y=43

Find x when y = -41

So this case is a bit different since we're given the y-value and not the x-value, and as I mentioned the equation represents the value of y in terms of x.

We still do a similar process, except we'll use some more algebraic manipulation, but let's start by plugging in the known value:

`-41=-4x+15`

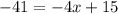
Let's move the constant, 15, to the other side by subtracting by 15 to cancel both sides.

`-56 = -4x`

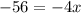
Now we want to get the x alone, and the only "operation" being done on the x, is that it's being multiplied by the coefficient of -4. To cancel this out we want to divide both sides by -4 to maintain equality & cancel out the coefficient of -4 to one, which is just 1 * x which can be expressed as x as it's implied the coefficient is 1

`14=x`

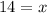
Now we have our solution!