The first thing we need to do is factor the denominators in the rational expressions.
Notice that in the denominator of the first rational expression we have a common factor

, so we can factor x out:

Now, the denominator of the second rational expression is a quadratic polynomial, we can factor it by finding tow numbers whose product will 21 and its sum will be 10. Those numbers are 7 and 3, (7x3=21 and 7+3=10):

Lets rewrite our rational expression with our factored denominators:
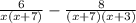
Now, to find the least common denominator we are going to take one of the common factors (x+7) and all the non-common factors: x and (x+3):
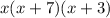
We can conclude that the correct answer is
a. x(x+7)(x+3)