Question

You probably have noticed that, as you increase ω, there will be a value, ωcrit, for which r(ω) goes to infinity. find ωcrit. answer in terms of k and m.

Answer 1

For the mass m, attached to a spring, to move in a circle centripetal force and restoring force of the spring must be equal. Centripetal force is given with this formula:

`F_c=(mv^2)/(r)=(mw^2r^2)/(r)=mw^2r`
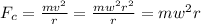
Restoring force only occurs if the spring is stretched. If L is the length of unstretched spring we have the following formula for restoring force:

`F=k(r-L)`
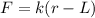
r is the length of a circle that mass m is traveling along.
As said above, these two forces have to be equal:

`F=k(r-L)=mw^2r`
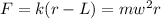
We solve for r:

`F=k(r-L)=mw^2r\\ kr-kL=mw^2r\\ mw^2r-kr=-kL\\ r(mw^2-k)=-kL\\ r=(-kL)/(mw^2-k)\\ r(w)=(kL)/(k-mw^2)`
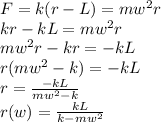
r(w) will go to infinity when denominator is equal to zero:

`k-mw^2=0\\ k=mw^2\\ w^2=(k)/(m)\\ w_(crit)=\sqrt{(k)/(m)}`
Please keep in mind that Hooke's law has it's limitations, and before we reach our critial value of angular velocity spring will be strecthed to a point where Hooke's law does not aply anymore.