Question

You flip a coin 10 times. Knowing that the event satisfies the requirements for a binomial distribution, find the probability that exactly 7 of the outcomes are heads.

Answer 1

Assuming a fair coin, and requirements for a binormial distribution are satisfied, then
p=0.50
n=20
The number of successes, x, is then given by
`P(x)=C(n,x)p^x(1-p)^(n-x)`where
`C(n,x)=(n!)/(x!(n-x)!)`
For x=7,

`P(x)=C(n,x)p^x(1-p)^(n-x)`

`P(7)=C(n,x)p^x(1-p)^(n-x)`

`=C(20,7)0.5^7(0.5)^(20-7)`

`=C(20,7)0.5^(20)`

`=(77520)/(1048576)`

`=(4845)/(65536)`

`=0.07393` to 5 places of decimal

Ans. the probability is 0.07393 to 5 places of decimal.

Answer 2

0.1172

Explanation:

The formula for the probability in a binomial distribution (n trials, r successes) is

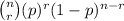`\binom{n}{r}(p)^r(1-p)^(n-r)` where p is the probability of success.

For flipping a coin, the probability of success, p, is 0.5.

The number of trials, n, is 10. The number of successes, r, is 7. This gives us

`\binom{10}{7}(0.5)^7(1-0.5)^(10-7)\\\\\binom{10}{7}(0.5)^7(0.5)^3=0.1171875 \approx 0.1172`