The first thing to is factor the denominator of the rational function:

to do this we'll need to find two number whose product is -3 and its sum is -2; those numbers are 1 and -3, so:
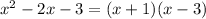
Now we can rewrite our rational function as follows:
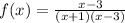
Notice that we have a common factor (x-3) in both numerator and denominator; therefore we can cancel them:

Taking all the above into consideration we realize that x=3 is a removable discontinuity; the correct answer is the first one: there is a hole in x=3 and asymptote at x=-1.