![\bf 3sin^2(\theta )+16sin(\theta )-35=0\impliedby \begin{array}{llll} \textit{notice this is just a quadratic }\\\\ax^2+bx+c=0 \end{array} \\\\\\\ [3sin(\theta )-5][sin(\theta )+7]=0\\\\ -------------------------------\\\\ 3sin(\theta )-5=0\implies 3sin(\theta )=5\implies sin(\theta )=\cfrac{5}{3} \\\\\\ \measuredangle \theta =sin^(-1)\left( (5)/(3) \right)](https://img.qammunity.org/2019/formulas/mathematics/college/khjw1ix1lrhyypq98dkhxe96tjykd0izsl.png)
now, before continuing on the first root, recall that the sine has a range of -1 ⩽ sin(θ) ⩽1, however 5/3 is greater than 1, and therefore is out of range, meaning, there's no such angle, so we've got zilch there.
now, let's check the second root,
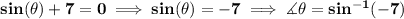
well, hell -7 is smaller than -1, so is also outside the range for sine, and so, the second root gave also zilch, so, in short, there's no such angle.