Question

Helppppppppppppppppppppppppppppppppppppppppppppppppp

Answer 1

we have
2[(16x³y)^(1/3)]+4[(54x³x³y³y²)^(1/3)]
2[(2³2x³y)^(1/3)]+4[(3³2x³x³y³y²)^(1/3)]
2[2x(2y)^(1/3)]+4[3x²y(2y)^(1/3)]
4x[(2y)^(1/3)]+12x²y[(2y)^(1/3)]
4x[(2y)^(1/3)]+12x²y[(2y)^(1/3)]

the answer is the option A) 4x[(2y)^(1/3)]+12x²y[(2y)^(1/3)]

Answer 2

Remember that for simplifying cube radicals, we need to factor the terms inside the radical to create cubes to match the cubic root of the radical, so we can take that term out it:
The first thing we are going to do is decompose the numbers 16 and 54 into prime factors:

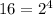
`16=2^(4)` and
`54=(2)(3^(3) )`
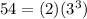
Now we are going to separate each term into cubes:

`2 ^(4) =(2)(2^(3) )`

`x ^(6) =( x^(3) )( x^(3) )`

`y^(5) =(y^(2))(y^(3) )`
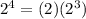
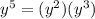
After that we can rewrite the expression:

`2( \sqrt[3]{(2)(2^(3))x^(3)y }) +4( \sqrt[3]{(2)( 3^(3))( x^(3))( x^(3))(y^(2))(y^3}) } )`
Finally we can take out the cubes and simplify:

`2(2)(x) \sqrt[3]{2y} +4(3)(x)(x)(y) \sqrt[3]{2 y^(2) }`

`4x \sqrt[3]{2y} +12 x^(2) y \sqrt[3]{2 y^(2) }`

The first choice,
`4x \sqrt[3]{2y} +12 x^(2) y \sqrt[3]{2 y^(2) }`, is the correct answer.