To multiply the imaginary number i, we still can use the product rule for exponents. When we multiply, we get
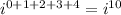
.
Now, simplifying this might seem formidable at first. But, let's start working through different powers of i.
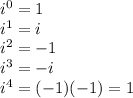
Notice that
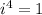
. That means that any power that is a multiply of four will also be 1. For instance,

, and so on...
If we rewrite

with this in mind, we can break it down into smaller pieces and simplify.
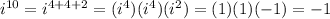 The answer is B.
The answer is B.