Question

Simplify completely quantity 4 x squared minus 32 x plus 48 all over quantity 3 x squared minus 17 x minus 6.

Answer 1

For this case we must simplify the following expression:

`\frac {4x ^ 2-32x + 48} {3x ^ 2-17x-6}`

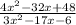
Simplifying the numerator, dividing all the terms by 4, we have:

`x ^ 2-8x + 12`

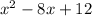
We factor by looking for two numbers that when added together give -8 and when multiplied by 12. These are: -6 and -2

`-6-2 = -8\\-6 * -2 = 12`

So, we have to:

`x ^ 2-8x + 12 = (x-6) (x-2)`

Simplifying the denominator:

We rewrite -17x as -18x + x:

`3x ^ 2-18x + x-6`

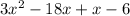
We factor the highest common denominator of each group:

`3x (x-6) +1 (x-6)`

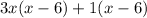
We factor the polynomial by factoring the highest common denominator (x-6):

`(x-6) (3x + 1)`

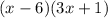
So, we have to:

`3x ^ 2-17x-6 = (x-6) (3x + 1)`

Substituting in the original expression we have:

`\frac {(x-6) (x-2)} {(x-6) (3x + 1)} = \frac {x-2} {3x + 1}`

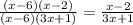
ANswer:

`\frac {4x ^ 2-32x + 48} {3x ^ 2-17x-6} = \frac {x-2} {3x + 1}`