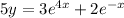Question

The given family of functions is the general solution of the differential equation on the indicated interval. find a member of the family that is a solution of the initial-value problem. y = c1e4x + c2e−x, (−∞, ∞); y'' − 3y' − 4y = 0, y(0) = 1, y'(0) = 2

Answer 1

Try this option (see the attachment), if it is possible check result in other sources.

Answer 2

The given differential equation is,

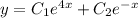`y=C_(1)e^(4 x)+C_(2)e^(-x)`------(A)

Differentiating once,with respect to x,

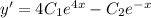`y'=4C_(1)e^(4 x)-C_(2)e^(-x)`-------(1)

Differentiating again with respect to x,

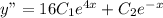`y`-------(2)

Equation (1) + Equation (2)

y' +y"
`=20 C_(1)e^(4 x)`

`C_(1)=(y'+y`

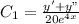
4 ×Equation (1) - Equation (2)

4 y'- y"
`=-5 C_(2)e^(-x)`

`C_(2)=(4y'-y`

Substituting the value of
`C_(1),C_(2)` in A,we get

`y=(y'+y`

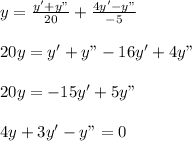
As, y(0)=1 , and y'(0)=2, gives

`C_(1)+C_(2)=1\\\\ 4C_(1)-C_(2)=2`

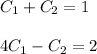
gives ,
`5C_(1)=3\\\\ C_(1)=(3)/(5)\\\\ 5 C_(2)=2\\\\ C_(2)=(2)/(5)`

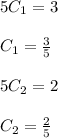
So, member of the family that is a solution of the initial-value problem,
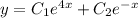`y=C_(1)e^(4 x)+C_(2)e^(-x)` is

`5 y=3 e^(4 x)+2 e^(-x)`