Here we have a projectile motion. It is type of motion that is made of a vertical shot and a horizontal shot. This is how we will solve it.
Firste step is to find horizontal and vertical component of a speed.
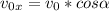
\\ v_{0y} = v_{0} * sin \alpha [/tex]
We are given this information:
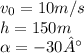
Angle is negative because it is below the horizontal.
VERTICAL SHOT
Time needed for a grenade to fall to the bottom of a building is given by a formula:
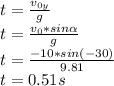
We used negative value for a speed because it is considered that upwards shot has positive value and downwards shot has negative value.
The grenade will not explode before it hits the ground.
HORIZONTAL SHOT
The horizontal distance from the building at which the grenade will land is called range. The formula for a range is given by:
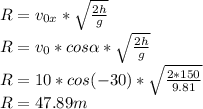
The grenade will hit the ground at distance of 47.89m.