Question

A circle has a diameter with endpoints (7, -7) and (5, -3). What is the equation of the circle?

Answer 1

For equation, we need 1) center, 2) radius
both can be found by using distance formula between 2 points:

`d = \sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) } \\ = \sqrt{ {(5 - 7)}^(2) + {( - 3 - - 7)}^(2) } \\ = \sqrt{ {(2)}^(2) + {(4)}^(2) } = √(4 + 16)`

`d = √(20) = √(4) * √(5) = 2 √(5)`
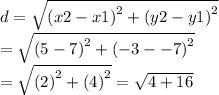
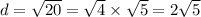
So our diameter is 2sr5, therefore our radius is half that: r = d/2 = 2sr5/2 = sr5
Now to calculate the center, go halfway between the x's and between the y's:
((7-5)/2 + 5, (-7--3)/2 + -3)
= ((2)/2 + 5, (-7+3)/2 + -3) = (1 + 5, (-4)/2 + -3)
= (1 + 5, -2 + -3) = (6, -5)
So our center is at (6, -5), where (h, k) is center for the formula, so h = 6, k = -5
Equation of a circle:

`{(x - h)}^(2) + {(y - k)}^(2) = {r}^(2) \\ {(x - 6)}^(2) + {(y + 5)}^(2) = {( √(5)) }^(2) \\ {(x - 6)}^(2) + {(y + 5)}^(2) = 5`