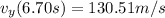Question

A plane, diving with constant speed at an angle of 40.9° with the vertical, releases a projectile at an altitude of 654 m. the projectile hits the ground 6.70 s after release. (a) what is the speed of the plane? (b) how far does the projectile travel horizontally during its flight? what were the magnitudes of the (c) horizontal and (d) vertical components of its velocity just before striking the ground? (state your answers to (c) and (d) as positive numbers.)

Answer 1

Let's solve the problem step-by-step.

A) Let's start writing the laws of motion on both x (horizontal) and y (vertical) axis. On the x-axis, it's a uniform motion with constant velocity, while on the y-axis it's an uniformly accelerated motion:

`S_x(t)=v_x t`

`S_y(t)=h-v_y t- (1)/(2) g t^2`
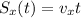
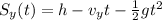
where h=654 m is the initial height of the projectile,
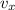
`v_x` and
`v_y` are the initial velocities on the x- and y-axis, g=9.81 m/s^2 and t is the time.
`v_y` ad
`g` have a negative signs because they both point downward.
We can calculate the initial velocity on the y-axis by requiring that
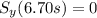
`S_y(6.70 s)=0`, since we know that after 6.70 s the projectile reached the ground. Therefore:

`0=h-v_yt- (1)/(2) gt^2=654 - 6.7 v_y - (1)/(2) (9.81)(6.70)^2`
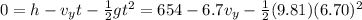
from which we find

`v_y=64.78 m/s`

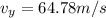
Then we can find the magnitude of the initial velocity v using the angle with respect to the vertical
`\alpha=40.9^(\circ)`:

`v_y = v cos \alpha`

`v= (v_y)/(cos \alpha) =85.7 m/s`

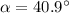
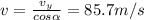
B) Let's calculate the component of the initial velocity on the x-axis:

`v_x = v sin \alpha = 85.7 m/s \cdot sin (40.9^(\circ))=56.11 m/s`
And then, we can find how far the projectile traveled horizontally by calculating Sx at t=6.70 s, when it hits the ground:

`S_x(6.70 s)=v_x t = 56.11 m/s \cdot 6.7 s=375.94 m`

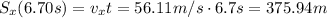
C) The horizontal component of the velocity does not change during the motion, since it's an uniform motion on the x-axis. Therefore, vx at t=6.7 s is the same as its initial value:

`v_x (6.70 s)=v_x = 56.11 m/s`

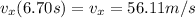
D) Instead, vy changes during the motion since it's an accelerated motion, following the law

`v_y(t) = - v_y -gt`
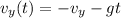
Using t=6.7 s, we can find the vertical velocity just before the projectile hits the ground

`v_y(6.70 s)= -64.78 m/s - (9.81 m/s^2)(6.70 s)=-130.51 m/s`
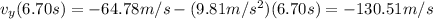
Writing it with positive sign:

`v_y(6.70 s) = 130.51 m/s`