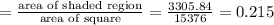Answer: C. 0.215
Explanation:
Given: A circle with a diameter of 124 m is inscribed in a square .
Thus side of square =124 m
Now, area of square=
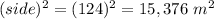
Radius of circle=
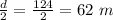
Area of circle=
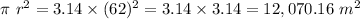
Now, Area of shaded region= Area of square-Area of circle
Area of shaded region=
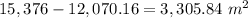
Probability that a point picked at random in the square is in the shaded region