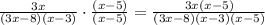we have the expression
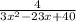
Rewrite as equivalent rational expressions with denominator (3x-8)(x-5)(x-3)
In this problem
3x^2-23x+40=3(x-5)(3x-8)
so
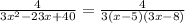
Multiply by (x-3)/(x-3)
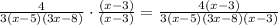
Part 2
we have the expression
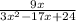
we have that
3x^2-17x+24=3(3x-8)(x-3)
so
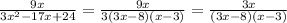
Multiply the expression by (x-5)/(x-5)