Question

Kiley and her parents traveled to visit her grandmother. They drove 24.3 miles from their house to the airport in 12 hour. At the airport, they exited the car and walked for 34 hour to the waiting area by the gate to board their plane. Their walk covered 1.2 miles. From the waiting area, they walked another 0.1 mile to board the plane. The plane left the gate 45 minutes after they arrived at the waiting area. The plane flew 346 miles in 214 hours. After the plane landed, Kiley and her parents walked for 30 minutes, covering 1.1 miles, before they found a cab. It was a 15-minute cab ride to get to Kiley’s grandmother’s house, which was 12.3 miles away.Answer the following questions about Kiley’s trip. All questions are written in terms of an average rate. Assume that an average rate includes the time that Kiley is at rest (that is, not moving).In this task, you will write the ratio of miles to hours for each leg of Kiley’s trip. You will then, express the ratio as a decimal number. Next, you will find the unit rate in miles per hour (mph) for each leg of the trip. If your unit rate includes a repeating decimal number, you must indicate which digits repeat (for example, write 0.3¯when the 3 repeats.) A description of each leg is listed below in parts A through F.

Answer 1

Given:

The car ride from Kiley's house to the airport.

Distance =24.3 miles.

Time =1/2 hour.

We know that

`\text{Average rate =}\frac{\text{Distance}}{\text{time}}`

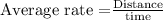
Substitute Distance =24.3 miles and time =1/2 hour to compute the average rate of the car ride from Kiley's house to the airport.

`=\frac{24.3\text{ miles}}{(1)/(2)\text{hours}}`
`\text{ Use }((a)/(b))/((c)/(d))=(a)/(b)*(d)/(c)\text{.}`

`=24.3*(2)/(1)\text{ miles per hour}`

`=24.3*2\text{ miles per hour}`
`=48.6\text{ miles per hour}`

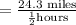
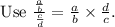
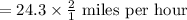
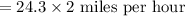
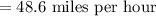
Hence the average rate of the car ride from Kiley's house to the airport is 48.6 miles per hour.

2)

Given that they walked 3/4 hours to the waiting area and covered the distance of 1.2 miles.

Distance =1.2 miles.

Time =3/4 hours.

we know that

`\text{Average rate =}\frac{\text{Distance}}{\text{time}}`

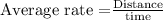
Substitute distance =1.2 miles and time =3/4 hours to compute the average rate of the walk from the car to the waiting area by the gate, at the airport.

`=\frac{1.2\text{ miles}}{(3)/(4)\text{ hours}}`

`=1.2*(4)/(3)\text{ miles per hour.}`

`=(1.2*4)/(3)\text{ miles per hour.}`

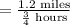
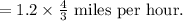
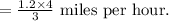
Multiplying 1.2 and 4, we get 4.8

`=(4.8)/(3)\text{ miles per hour.}`

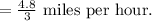
Dividing 4.8 by 3, we get 1.6

`=1.6\text{ miles per hour.}`

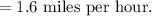
Hence at the airport, the average rate of the walk from the car to the waiting area by the gate is 1.6 miles per hour.