Answer:
Option A ic orrect.

Explanation:
Point slope form:
The equation of line is given by:
 .....[1]
.....[1]
where m is the slope of line and a point
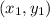 lies on the line in the coordinate plane.
lies on the line in the coordinate plane.
As per the statement:
You can see from the graph of line
We have two points i.e,
(0, 4) and (7, 1)
First calculate the slope:

then;

Now, substitute the value of m and (0,4) in [1] we have;
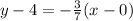
Simplify:
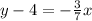
Add 4 to both sides we get;

Therefore, the equation best represents the trend line for the scatter plot is
