Question

Is the point (1,3) a solution to the linear equation 5x-9y=32? explain

Answer 1

5x-9y=32
P (1,3)
Substitute:
5*(1)-9*(3)=32
5-27=32
-22=32 which is impossible.
Then the point (1,3) is not a solution.

Answer 2

There are many ways to check if the point (1,3) is a solution to the linear equation
`5x-9y=32`.

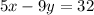Let us check it by expressing y in terms of x.

The given expression is 5x-9y=32. If we add -5x to both sides we will get:

`-9y=-5x+32`

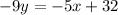
Multiplying both sides by -1 we will get:

`9y=5x-32`

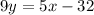
In order to isolate y, we will divide both sides by 9 to get:

`y=(5)/(9)x-(32)/(9)`

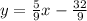
Now let us plug in the given value of x=1 from the point (1,3). This should give us y=3. Let us see if we get y=3 when we plug x=1 in the above equation.

`y=(5)/(9)* 1-(32)/(9)=(5-32)/(9)`

`\therefore y=(-27)/(9)=-3`

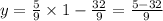
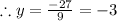
Thus, we see that when x=1, y=-3 and that
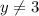`y\\eq 3` and hence we conclude that the point (1,3) is not a solution to the original given linear equation 5x-9y=32.

For a better understanding of the explanation given here a graph has been attached. As can be seen from the graph, (1,3) does not lie on the straight line that represents 5x-9y=32, but (1,-3) does lie on it as we had just found out.