Answer:
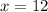
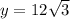
Explanation:
We have been given diagram of a triangle. We are asked to find the values of x and y for the given triangle.
We will use law of trigonometric ratios to find the sides of our given triangle.
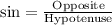
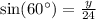
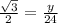
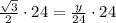
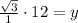
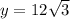
Therefore, the value of y is
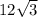 .
.
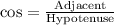
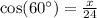
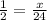
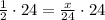
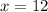
Therefore, the value of x is 12.