Question

Determine whether the point (1, 5) is a solution to the system of equations. Explain your reasoning in complete sentences. graph of a line 3 times x plus 2 and the absolute value of x minus 1 plus one. The graphs intersect at the point 0 comma 2.

Answer 1

According to your text first equation is
y = 3x+2
second equation is
y = Ix-1I + 1

Definition of our absolute value Ix-1I is
1) we take x-1 with condition x-1≥0 => x≥1
2) we take -(x-1) = -x+1 with x<1

Let's form the first system with condition x≥1
y= 3x+2 and y=x-1+1=> y=x
If the left sides of the equations are equal, than the right sides are equal too
3x+2=x => 3x-x=-2 => 2x=-2 => x=-1
This solution we can't accept because it does not meet the condition
x≥1
Lets's form the second system with condition x<1
y=3x+2 and y= -x+1+1 =. y = -x+2
In the same way as previous the right sides are equal =>
3x+2=-x+2 => 3x+x = +2-2 => 4x=0 => x=0
We accept this solution bacause its meet with condition x<1
When we replace this solution in equation y=3x+2 we got
y=3*0+2=2 Only one solution is (x,y) = (0,2)
Good luck !!!!!

Answer 2

No

Explanation:

We are given that two equations

`y= 3x+2`

`y=\mid{x-1}\mid+1`

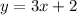
We have to check point (1,5) is a solution of given system of equations.

If at point (1,5) ,the two equations have same value then the point is a solution of system of equations.

Substitute x=1 then we get

`y=3(1)+2=5`

`y=\mid{1-1}\mid+1=1`

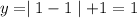
If we are substituting x=1 then equation give value of y =5 but second equation does not give 5 .Hence , the point (1,5) is not the solution to the system of equation.Because given point does not satisfied the second equation.