Answer:
- (f/g)(x) = 4x^3 +x^2 -5x +10
- (f/g)(1) = 10
Explanation:
You want to find the rational function (f/g)(x) and its value for x=1 when f(x) = 4x^4−19x^3−10x^2+35x−50 and g(x) = x-5.
Polynomial division
The ratio function is the ratio of the given functions, found by dividing f(x) by g(x). Since g(x) is a binomial with a leading coefficient of 1, synthetic division is recommended. The attachment shows the result.
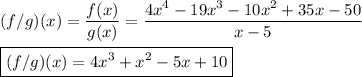
The value of this function when x=1 is ...
(f/g)(1) = 4·1³ +1² -5·1 +10 = 4 +1 -5 +10
(f/g)(1) = 10