Question

Find the perimeter of triangle PQR. Round your answer to the nearest tenth.

19.7 units
16 units
8 units
7.2 units

Answer 1

for pq, you can count the lenght, so pq=8
pythAGOREAN THEOREM or distance formula to solve
Look them up if you don't know them
i got 19.68

Answer 2

Answer: The correct option is

(A) 19.7 units.

Step-by-step explanation: We are given to find the perimeter of triangle PQR and round the answer to the nearest tenth.

From the figure, we note that the co-ordinates of the vertices of triangle PQR are P(-2, 1), Q(6, 1) and R(4, -3).

We know that the perimeter of a triangle is equal to the sum of the lengths of its three sides.

The lengths of the sides PQ, QR and PR can be calculated using distance formula as follows :

`PQ=√((6+2)^2+(1-1)^2)=√(8^2)=8,\\\\QR=√((4-6)^2+(-3-1)^2)=√(4+16)=√(20)=2\sqrt5=4.4721,\\\\PR=√((4+2)^2+(-3-1)^2)=√(36+16)=√(52)=2√(13)=7.2111.`

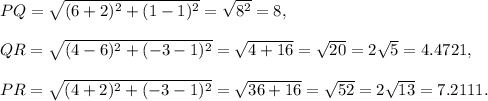
Therefore, the perimeter of triangle PQR is given by

`p=PQ+QR+PR=8+5.4721+7.2111=19.6832.`

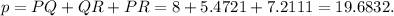
Rounding to the nearest tenth, we get

p = 19.7 units.

Thus, the required perimeter of triangle PQR is 19.7 units.

Option (A) is CORRECT.