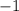Answer:
Given the equation:
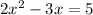
Subtract 5 from both sides we get;
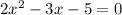
Factorize the equation:
Break the middle term we get;
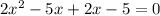
⇒
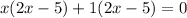
Take (2x-5) common we have;
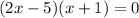
By zero product property we have;
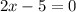 or
or
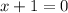
⇒
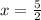 or x = -1
or x = -1
Therefore, the solutions for the given equation are:
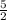 ,
,