1) Let's put
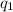
and
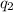
both on the x-axis such that
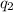
is on the right side of
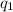
. The distance between the two charges is
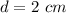
.
2) Let's put
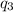
on the x-axis and let's call

the distance between charge 1 and charge 3. As a consequence, the distance between charge 2 and 3 will be
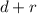
: if r is positive, then charge 3 will be located on the left of charge 1, if r is negative, charge 3 will be located between charge 1 and charge 2.
3) The electrostatic force between charge 1 and charge 3 is
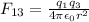
while the force between charge 2 and charge 3 is
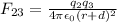
4) The problem says the two forces are equal in intensity. Therefore we can write
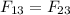
. Using the equations written at step 3), and substituting
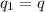
and
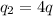
as mentioned in the problem,
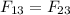
becomes
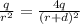
Using
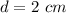
, we can solve the equation, and we get two solutions:
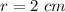
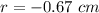
Both solutions are correct. With the former, the charge 3 is located 2 cm on the left of charge 1, while with the latter, charge 3 is located 0.67 cm on the right of charge 1, between charge 1 and 2.