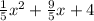Answer:
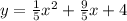or y = 1/5x^2+9/5x+4 (they are the same just different formats)
Explanation:
In this case we are given the intercepts of the parabola (aka another name for a quadratic function). Since the intercepts are given, it makes the most sense to use intercept form.
The basic formula for intercept form is:
y=a(x-b)(x-c) where a, b, and c are all constants
b and c are the x intercept values.
plug in the values:
y=a(x-(-4))(x-(-5))=a(x+4)(x+5)
y=a(x+4)(x+5) let's call this equation 1
unfortunately, there is still an "a" at the beginning, but that's where the y intercept is used.
Since (0,4) is a solution to the equation: y=a(x+4)(x+5), the values can be plugged into this equation to solve for a.
In this case, x = 0 and y = 4, so plug in those values
4=a(0+4)(0+5) = a(4)(5) = 20a
a = 1/5
Now, plug "a" back into equation 1
y=1/5(x+4)(x+5) this is the intercept form. However, the question ask for standard form, so it must be expanded
FOIL the parentheses (expand it) to get:
y=1/5(x^2+9x+20) =
