Question

what is the polynomial function of lowest degree with leading coefficient of 1 and roots 2 and 1 + square root2

Answer 1

f(x)=x^3-4x^2+3x+2

(Third answer)

Explanation:

I got a 100% on the test (Edge) and had this same exact question (:

Answer 2

If the roots to such a polynomial are 2 and
`1+\sqrt2`, then we can write it as


`(x-2)(x-(1+\sqrt2))`

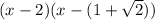
courtesy of the fundamental theorem of algebra. Now expanding yields


`(x-2)(x-1-\sqrt2)=x^2-2x-(1+\sqrt2)x+2(1+\sqrt2)=x^2-(3+\sqrt2)x+2+2\sqrt2`

which would be the correct answer, but clearly this option is not listed. Which is silly, because none of the offered solutions are *the* polynomial of lowest degree and leading coefficient 1.

So this makes me think you're expected to increase the multiplicity of one of the given roots, or you're expected to pull another root out of thin air. Judging by the choices, I think it's the latter, and that you're somehow supposed to know to use
`1-\sqrt2` as a root. In this case, that would make our polynomial


`(x-2)(x-(1+\sqrt2))(x-(1-\sqrt2))=x^3-4x^2+3x+2`

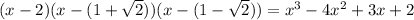
so that the answer is (probably) the third choice.

Whoever originally wrote this question should reevaluate their word choice...