Which function is the same as y=3cos(2(x+pi/2))-2? - QAmmunity.org

Which function is the same as y=3cos(2(x+pi/2))-2?

asked Aug 26, 2019 10.0k views

2 Answers

Answer:

Option B is Correct.

Explanation:

Given:
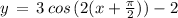
$y\,=\,3\,cos\,(2(x+(\pi)/(2)))-2$

To find: Equivalent Expression.

We use Following functions:

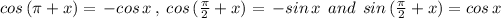
$cos\,(\pi+x)=\,-cos\,x\:,\:cos\,((\pi)/(2)+x)=\,-sin\,x\:\:and\:\:sin\,((\pi)/(2)+x)=cos\,x$

First we simply the given expression,

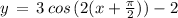
$y\,=\,3\,cos\,(2(x+(\pi)/(2)))-2$

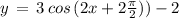
$y\,=\,3\,cos\,(2x+2(\pi)/(2)))-2$

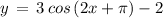
$y\,=\,3\,cos\,(2x+\pi)-2$

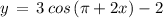
$y\,=\,3\,cos\,(\pi+2x)-2$

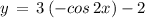$y\,=\,3\,(-cos\,2x)-2$ ( using above mentioned result )

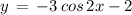$y\,=\,-3\,cos\,2x-2$ ............................(1)

Option A:

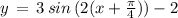
$y\,=\,3\,sin\,(2(x+(\pi)/(4)))-2$

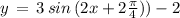
$y\,=\,3\,sin\,(2x+2(\pi)/(4)))-2$

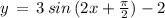
$y\,=\,3\,sin\,(2x+(\pi)/(2))-2$

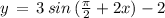
$y\,=\,3\,sin\,((\pi)/(2)+2x)-2$

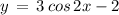$y\,=\,3\,cos\,2x-2$ ( using above mentioned result )

Since, it is not equal to (1)

Therefore, It is Not correct Option.

Option B:

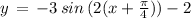
$y\,=\,-3\,sin\,(2(x+(\pi)/(4)))-2$

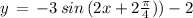
$y\,=\,-3\,sin\,(2x+2(\pi)/(4)))-2$

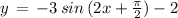
$y\,=\,-3\,sin\,(2x+(\pi)/(2))-2$

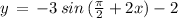
$y\,=\,-3\,sin\,((\pi)/(2)+2x)-2$

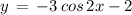$y\,=\,-3\,cos\,2x-2$ ( using above mentioned result )

Since, it is equal to (1)

Therefore, It is Correct Option.

Option C:

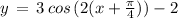
$y\,=\,3\,cos\,(2(x+(\pi)/(4)))-2$

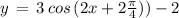
$y\,=\,3\,cos\,(2x+2(\pi)/(4)))-2$

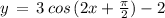
$y\,=\,3\,cos\,(2x+(\pi)/(2))-2$

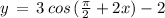
$y\,=\,3\,cos\,((\pi)/(2)+2x)-2$

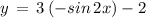$y\,=\,3\,(-sin\,2x)-2$ ( using above mentioned result )

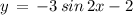
$y\,=\,-3\,sin\,2x-2$

Since, it is not equal to (1)

Therefore, It is Not correct Option.

Option D:

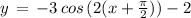
$y\,=\,-3\,cos\,(2(x+(\pi)/(2)))-2$

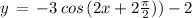
$y\,=\,-3\,cos\,(2x+2(\pi)/(2)))-2$

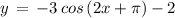
$y\,=\,-3\,cos\,(2x+\pi)-2$

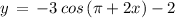
$y\,=\,-3\,cos\,(\pi+2x)-2$

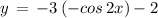$y\,=\,-3\,(-cos\,2x)-2$ ( using above mentioned result )

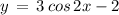
$y\,=\,3\,cos\,2x-2$

Since, it is not equal to (1)

Therefore, It is Not correct Option.

Therefore, Option B is Correct.

Sam Berry answered Aug 31, 2019

5.9k points

Search QAmmunity.org