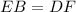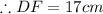Question

ABCD is a parallelogram such that AB is parallel to DC and DA parallel to CB. The length of side AB is 20 cm. E is a point between A and B such that the length of AE is 3 cm. F is a point between points D and C. Find the length of DF such that the segment EF divide the parallelogram in two regions with equal areas

Answer 1

The length of DF will be 17 cm.

Answer 2

`\therefore DF=17cm`

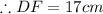
Explanation:

The easiest way to solve this, it's by graphing.

By given, we know that

`AB=20cm`, and
`AE=3cm`.

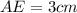By sum of segments, we have

`AE+EB=AB\\3cm+EB=20cm\\EB=20cm-3cm\\EB=17cm`

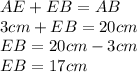
Additionally, we know that segment EF divides the parallelogram in two equal areas, that is, in two equal trapezoids, that means their bases are congruent.

So,

`EB=DF`

`\therefore DF=17cm`