Question

In ΔXYZ, y = 75 cm, z = 83 cm and ∠X=157°. Find the length of x, to the nearest centimeter.

Answer 1

x = 155 cm

Explanation:

The Law of Cosines

It relates the length of the sides of a triangle with one of its internal angles.

Let x,y, and z be the length of the sides of a given triangle, and X the included angle between sides y and z, then the following relation applies:

`x^2=y^2+z^2-2yz\cos X`

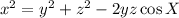
It's given: y=75 cm, z=83 cm, and
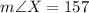`m\angle X=157` ° . Applying the formula:

`x^2=75^2+83^2-2*75*83\cos 157^\circ`

Calculating:

`x^2=5625+6889-12450(-0.9205)`

`x^2=23974.225`

`x=√(23974.225)`

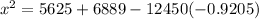
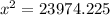
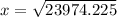
x = 155 cm