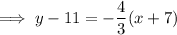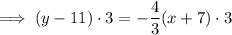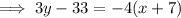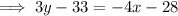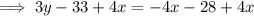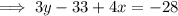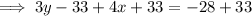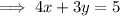Question

A line is drawn through (-7, 11) and (8,-9). The equation

y-11 = -4/3(x + 7) is written to represent the line. Which
equations also represent the line? Check all that apply.

Answer 1

`\textsf{Slope-intercept form}: \quad y=-(4)/(3)x+(5)/(3)`

`\textsf{Standard form}: \quad 4x+3y=5`

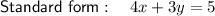
Explanation:

Given linear equation:

`y-11=-(4)/(3)(x+7)`

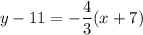
The given linear equation is point-slope form.

`\boxed{\begin{minipage}{3.7cm}\underline{Slope-intercept form}\\\\$y=mx+b$\\\\where $m$ is the slope\\ and $b$ is the $y$-intercept.\\\end{minipage}}`

To write the equation in slope-intercept form, isolate y:

`\implies y-11=-(4)/(3)(x+7)`

`\implies y-11=-(4)/(3)x-(28)/(3)`

`\implies y-11+11=-(4)/(3)x-(28)/(3)+11`

`\implies y=-(4)/(3)x+(5)/(3)`

`\boxed{\begin{minipage}{5.4 cm}\underline{Standard form}\\\\$Ax+By=C$\\\\where $A, B$ and $C$ are constants and $A$ must be positive.\\\end{minipage}}`

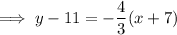
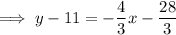
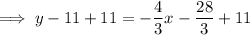
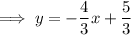
To write the equation in standard form, eliminate the fraction, bring the terms in x and y to the left of the equation, and the constants to the right:

`\implies y-11=-(4)/(3)(x+7)`

`\implies (y-11) \cdot 3=-(4)/(3)(x+7) \cdot 3`

`\implies 3y-33=-4(x+7)`

`\implies 3y-33=-4x-28`

`\implies 3y-33+4x=-4x-28+4x`

`\implies 3y-33+4x=-28`

`\implies 3y-33+4x+33=-28+33`

`\implies 4x+3y=5`