Question

Identify the horizontal asymptote of f(x) =3/5x

Answer 1

ANSWER

The horizontal asymptote is

`y = 0`



EXPLANATION

The given function is

`f(x) = (3)/(5x)`

This is a rational function which can be rewritten as,



`f(x) = (0x + 3)/(5x)`


The horizontal asymptote can be found by expressing the coefficient of

`x`

in the numerator over the coefficient of

`x`
in the denominator.



Thus the horizontal asymptote is,

`y = (0)/(5)`
This simplifies to

`y = 0`

Therefore the horizontal asymptote of the given rational function coincides with the x-axis.


It is the red straight line in the attachment.

Answer 2

y=0

Explanation:

We are given that a rational function

`f(x)=(3)/(5)x`

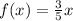
We have to find the horizontal asymptote of the given function.

The function can be written as

`f(x)=(3x^0)/(5x)`

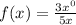
Degree of numerator polynomial=0

Degree of denominator polynomial=1

Degree of numerator polynomial is less than the degree of denominator polynomial.

When degree of numerator polynomial is less than the degree of denominator polynomial then,

Horizontal asymptote=y=0

Therefore, horizontal asymptote=0