Question

The base of a triangle is one third as long as its height. if the area of the triangle is 6 square meters, how long is its base

Answer 1

The answer is: " 2 m" .
________________________________________
Explanation:
_________________________________________
The formula for the area, "A" , of a TRIANGLE is:
_________________________________________
A = (1/2) * b * h ; or, write as: " A = (b * h) / 2 " ;
_________________________________________
in which: A = area of triangle;
b = length of base;
h = [perpendicular] height .
_________________________________________
We are given: "b = 1/3 h = h/3" ;
"A = 6 m²: "

We are asked to solve for "b" ;

So: "A = ( b * h) / 2 " ;

→ Re-arrange the equation to isolate "b" on one side of the equation ;

→ "A = ( b * h) / 2 " ; ;

Multiply EACH SIDE of the equation by "2" ;
→ 2 * A = { ( b * h) / 2 } * 2 " ;

to get:

→ 2A = b * h ;

↔ b * h = 2A ;

NOTE: Calculate "2A" ; as follows: " 2A = 2* 6 m² = 12 m² " ;

→ b * h = 12 m² ;

Note: "b = h/3 " ;

So rewrite:

→ "b * h = 12 m² ;

as: (h/3) * h = 12 m² ;

→
`(h)/(3)` *
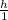
`(h)/(1)` = 12 m² ;

→
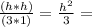
`((h*h))/((3*1)) = (h^2)/(3) =` = 12 ;

→ Now, we can solve for "h" ; {and then, solve for "b" }..
___________________________________________________
We have: \frac{h^2}{3} = [/tex] = 12
______________________________________________________
→ h² = 12 * 3 ;

→ h² = 36 ;

Now, take the positive square root of EACH SIDE of the equation;
to isolate "h" on one side of the equation; & to solve for "h" ;

→ +√(h²) = +√36 ;

→ h = 6 m ;

Now, we can solve for "b" ;

b = h / 3 = 6 m / 3 = 2 m .

→ b = 2 m .
________________________________________

The answer is: " 2 m" .
________________________________________
Let us check our answer:
________________________________________
A = (b * h) / 2 ;

→ 6 m² = ? (2 m * 6 m) / 2 ?? ;

→ 6 m² = ? (12 m²) / 2 ?? Yes!
________________________________________